Page 139 - Math Course 2 (Book 2)

Triangle Inequality Theorem

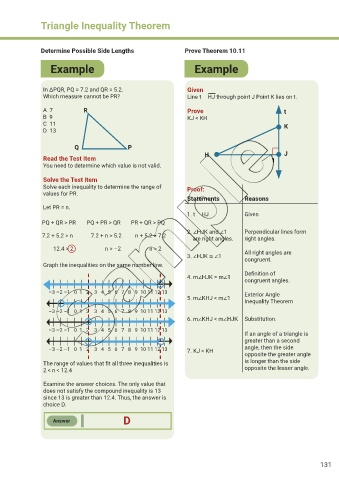
Determine Possible Side Lengths Prove Theorem 10.11

Example Example

In ΔPQR, PQ = 7.2 and QR = 5.2. Given
Which measure cannot be PR? Line t ⟂ HJ through point J Point K lies on t.

A 7 R Prove t
B 9 KJ < KH
C 11 K
D 13

Q P
H J
Read the Test Item 1
You need to determine which value is not valid.

Solve the Test Item
Solve each inequality to determine the range of Proof:
values for PR.
Statements Reasons
Let PR = n.
1. t ⟂ HJ Given
PQ + QR > PR PQ + PR > QR PR + QR > PQ
2. ∠HJK and ∠1 Perpendicular lines form
7.2 + 5.2 > n 7.2 + n > 5.2 n + 5.2 > 7.2 are right angles. right angles.

12.4 > 2 n > –2 n > 2 All right angles are
3. ∠HJK ≅ ∠1 congruent.
Graph the inequalities on the same number line.
Definition of
4. m∠HJK = m∠1
congruent angles.
–3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Exterior Angle
5. m∠KHJ < m∠1
Inequality Theorem
–3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 11 12 13
6. m∠KHJ < m∠HJK Substitution.

–3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 11 12 13
If an angle of a triangle is
greater than a second
–3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 7. KJ < KH angle, then the side
opposite the greater angle
The range of values that fit all three inequalities is is longer than the side
2 < n < 12.4 opposite the lesser angle.

Examine the answer choices. The only value that
does not satisfy the compound inequality is 13
since 13 is greater than 12.4. Thus, the answer is
choice D.
D
Answer

131