Page 167 - Math Course 1 (Book 1)

Inequalities: Addition and Subtraction

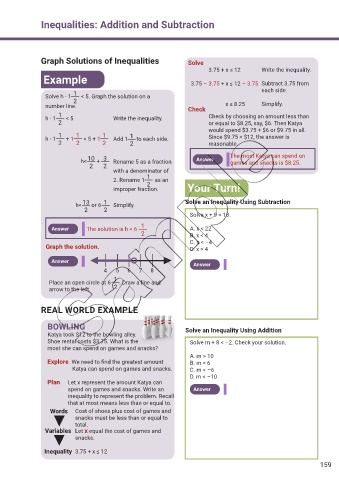
Graph Solutions of Inequalities Solve
3.75 + x ≤ 12 Write the inequality.
Example 3.75 – 3.75 + x ≤ 12 – 3.75 Subtract 3.75 from

each side.
1
Solve h - 1 < 5. Graph the solution on a
2
number line. Check x ≤ 8.25 Simplify.
1 Check by choosing an amount less than
h - 1 < 5 Write the inequality.
2 or equal to $8.25, say, $6. Then Katya
would spend $3.75 + $6 or $9.75 in all.
1 1 1 1 Since $9.75 < $12, the answer is
h - 1 + 1 < 5 + 1 Add 1 to each side.
2 2 2 2 reasonable.

10 3 Answer The most Katya can spend on
h< + Rename 5 as a fraction games and snacks is $8.25.
2 2
with a denominator of
1
2. Rename 1 as an
2
improper fraction. Your Turn!

13 1 Solve an Inequality Using Subtraction
h< or 6 Simplify.
2 2
Solve x + 9 < 13.
1
Answer The solution is h < 6 A. x < 22
2 B. x < 4
C. x < –4
Graph the solution. D. x > 4

Answer
Answer
4 5 6 7 8
1
Place an open circle at 6 . Draw a line and
arrow to the left. 2

REAL WORLD EXAMPLE

BOWLING Solve an Inequality Using Addition

Katya took $12 to the bowling alley.
Shoe rental costs $3.75. What is the Solve m + 8 < –2. Check your solution.
most she can spend on games and snacks?
A. m > 10
Explore We need to f nd the greatest amount B. m < 6
Katya can spend on games and snacks. C. m < –6
D. m < –10
Plan Let x represent the amount Katya can
spend on games and snacks. Write an Answer
inequality to represent the problem. Recall
that at most means less than or equal to.
Words Cost of shoes plus cost of games and
snacks must be less than or equal to
total.
Variables Let x equal the cost of games and
snacks.

Inequality 3.75 + x ≤ 12

159