Page 81 - Math Course 1 (Book 2)

Midpoints of a Segment

Mo. 9

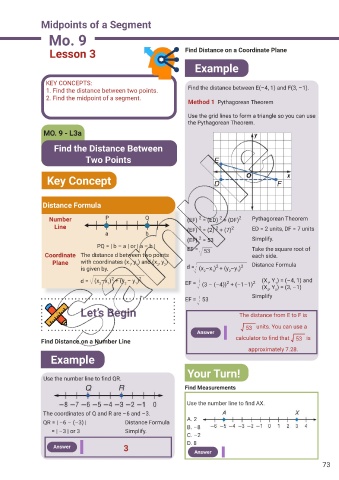
Lesson 3 Find Distance on a Coordinate Plane

Example

KEY CONCEPTS:
1. Find the distance between two points. Find the distance between E(–4, 1) and F(3, –1).
2. Find the midpoint of a segment.
Method 1 Pythagorean Theorem

Use the grid lines to form a triangle so you can use
the Pythagorean Theorem.
MO. 9 - L3a

Find the Distance Between

Two Points

Key Concept

Distance Formula

2
Number P Q (EF) = (ED) + (DF) 2 Pythagorean Theorem
2
Line (EF) = (2) + (7) 2 ED = 2 units, DF = 7 units
2
2
a b
2
(EF) = 53 Simplify.
PQ = | b – a | or | a – b |
EF = 53 Take the square root of
Coordinate The distance d between two points each side.
Plane with coordinates (x , y ) and (x , y ) Distance Formula
2
2
1
1
2
is given by. d = (x –x ) + (y –y ) 2
2
1
1
2
2
d = (x –x ) + (y – y ) 2 (X , Y ) = (–4, 1) and
2
2 1 2 1 EF = (3 – (–4)) + (–1–1) 2 1 1
(X , Y ) = (3, –1)
2 2
Simplify
EF = 53
Let’s Begin The distance from E to F is
units. You can use a
53
Answer
calculator to f nd that is
53
Find Distance on a Number Line
approximately 7.28.
Example
Your Turn!
Use the number line to f nd QR.
Find Measurements
Use the number line to f nd AX.
The coordinates of Q and R are –6 and –3.
A. 2
QR = | –6 – (–3) | Distance Formula
B. –8
= | –3 | or 3 Simplify.
C. –2
D. 8
Answer 3
Answer
73