Page 21 - Math Course 2 (Book 2)

Geometric Volume: Pyramids and Cones
Mo. 7

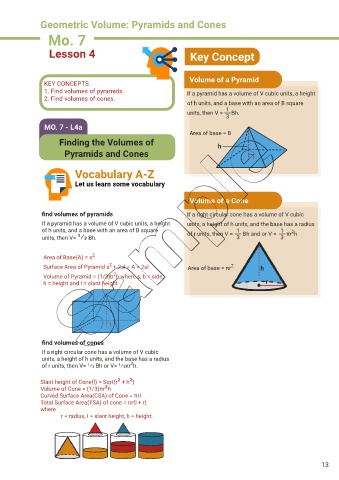
Lesson 4 Key Concept

Volume of a Pyramid
KEY CONCEPTS:
1. Find volumes of pyramids. If a pyramid has a volume of V cubic units, a height
2. Find volumes of cones.
of h units, and a base with an area of B square
1
units, then V = Bh.
3
MO. 7 - L4a
Area of base = B
Finding the Volumes of h
Pyramids and Cones

Vocabulary A-Z

Let us learn some vocabulary

Volume of a Cone

find volumes of pyramids If a right circular cone has a volume of V cubic
If a pyramid has a volume of V cubic units, a height units, a height of h units, and the base has a radius
1
of h units, and a base with an area of B square of r units, then V = Bh and or V = πr h
1
2
units, then V= 1/3 Bh. 3 3
Area of Base(A) = s 2
2
Surface Area of Pyramid s + 2sl = A + 2sl Area of base = πr 2 h
2
Volume of Pyramid = (1/3)b h where s, b = side,
h = height and I = slant height. r

find volumes of cones
If a right circular cone has a volume of V cubic
units, a height of h units, and the base has a radius
2
of r units, then V= 1/3 Bh or V= 1/3πr h.

Slant height of Cone(I) = Sqrt(r² + h²)
Volume of Cone = (1/3)πr²h
Curved Surface Area(CSA) of Cone = πrl
Total Surface Area(TSA) of cone = πr(l + r)
where
r = radius, I = slant height, h = height.

13