Page 26 - Math Course 2 (Book 2)

Congruent and Similar Solids

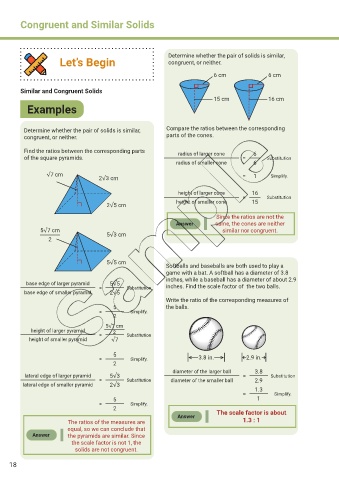
Let’s Begin Determine whether the pair of solids is similar,
congruent, or neither.

6 cm 6 cm

Similar and Congruent Solids
15 cm 16 cm
Examples

Determine whether the pair of solids is similar, Compare the ratios between the corresponding
congruent, or neither. parts of the cones.

Find the ratios between the corresponding parts radius of larger cone 6
of the square pyramids. = Substitution
radius of smaller cone 6
√7 cm = 1 Simplify.
2√3 cm

height of larger cone 16
= Substitution
height of smaller cone 15
2√5 cm
Since the ratios are not the
Answer same, the cones are neither
5√7 cm 5√3 cm similar nor congruent.
2

5√5 cm
Softballs and baseballs are both used to play a
game with a bat. A softball has a diameter of 3.8
inches, while a baseball has a diameter of about 2.9
base edge of larger pyramid 5√5
= Substitution inches. Find the scale factor of the two balls.
base edge of smaller pyramid 2√5
Write the ratio of the corresponding measures of
5 the balls.
= Simplify.
2
5√7 cm
height of larger pyramid 2
height of smaller pyramid = √7 Substitution

5
= Simplify. 3.8 in. 2.9 in.
2
diameter of the larger ball 3.8
lateral edge of larger pyramid 5√3 = Substitution
lateral edge of smaller pyramid = 2√3 Substitution diameter of the smaller ball 2.9
1.3
≈ Simplify.
5 1
= Simplify.
2
Answer The scale factor is about
The ratios of the measures are 1.3 : 1
equal, so we can conclude that
Answer the pyramids are similar. Since
the scale factor is not 1, the
solids are not congruent.

18