Page 71 - Math Course 3 (Book 1)

Exponential Growth and Decay

Mo. 2

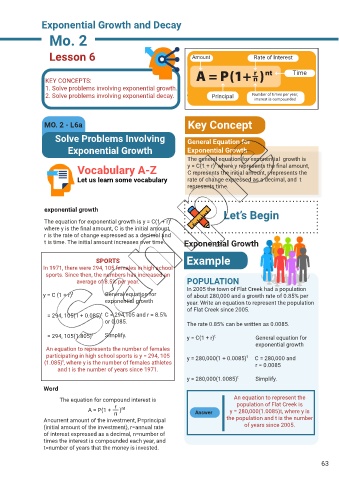
Lesson 6 Amount Rate of Interest

Time
KEY CONCEPTS:
1. Solve problems involving exponential growth.
2. Solve problems involving exponential decay. Principal Number of times per year,
interest is compounded

MO. 2 - L6a Key Concept

Solve Problems Involving General Equation for

Exponential Growth Exponential Growth
The general equation for exponential growth is
t
Vocabulary A-Z y = C(1 + r) where y represents the final amount,
C represents the initial amount, r represents the
Let us learn some vocabulary rate of change expressed as a decimal, and t
represents time.

exponential growth Let’s Begin

t
The equation for exponential growth is y = C(1 + r)
where y is the final amount, C is the initial amount,
r is the rate of change expressed as a decimal and
t is time. The initial amount increases over time. Exponential Growth

SPORTS Example
In 1971, there were 294, 105 females in high school
sports. Since then, the numbers has increased an
average of 8.5% per year. POPULATION
In 2005 the town of Flat Creek had a population
y = C (1 + r) t General equation for of about 280,000 and a growth rate of 0.85% per
exponential growth year. Write an equation to represent the population
of Flat Creek since 2005.
= 294, 105(1 + 0.085) C = 294,105 and r = 8.5%
t
or 0.085. The rate 0.85% can be written as 0.0085.

= 294, 105(1.805) t Simplify. y = C(1 + r) t General equation for
exponential growth
An equation to represents the number of females
participating in high school sports is y = 294, 105 y = 280,000(1 + 0.0085) C = 280,000 and
t
t
(1.085) , where y is the number of females athletes r = 0.0085
and t is the number of years since 1971.
t
y = 280,000(1.0085) Simplify.
Word

The equation for compound interest is An equation to represent the
r population of Flat Creek is
A = P(1 + ) nt y = 280,000(1.0085)t, where y is
n Answer
A=current amount of the investment, P=principal the population and t is the number
(initial amount of the investment), r=annual rate of years since 2005.
of interest expressed as a decimal, n=number of
times the interest is compounded each year, and
t=number of years that the money is invested.

63