Page 11 - Math Course 1 (Book 2)

Properties of Identity and Equality

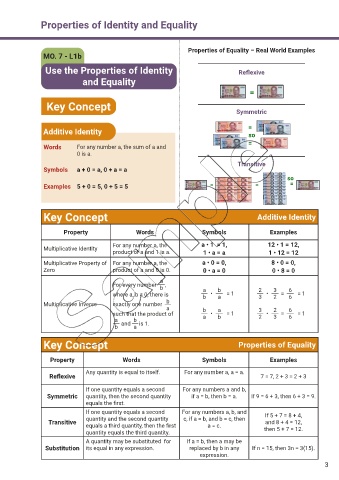
Properties of Equality – Real World Examples
MO. 7 - L1b

Use the Properties of Identity Ref exive

and Equality Reflexive
=

Key Concept
Symmetric
Symmetric
=
Additive Identity so

=
Words For any number a, the sum of a and
0 is a.
Transitive
Symbols a + 0 = a, 0 + a = a Transitive
so
Examples 5 + 0 = 5, 0 + 5 = 5 = = =

Key Concept Additive Identity

Property Words Symbols Examples

For any number a, the a • 1 = 1, 12 • 1 = 12,
Multiplicative Identity
product of a and 1 is a. 1 • a = a 1 • 12 = 12
Multiplicative Property of For any number a, the a • 0 = 0, 8 • 0 = 0,
Zero product of a and 0 is 0. 0 • a = 0 0 • 8 = 0

a
For every number ,
b a b 2 3 6
where a, b ≠ 0, there is b • a = 1 3 • 2 = 6 = 1
b
Multiplicative Inverse exactly one number
a b a 3 2 6
such that the product of a • b = 1 2 • 3 = 6 = 1
a b
and is 1.
b a

Key Concept Properties of Equality

Property Words Symbols Examples

Any quantity is equal to itself. For any number a, a = a.
Ref exive 7 = 7, 2 + 3 = 2 + 3

If one quantity equals a second For any numbers a and b,
Symmetric quantity, then the second quantity if a = b, then b = a. If 9 = 6 + 3, then 6 + 3 = 9.
equals the f rst.
If one quantity equals a second For any numbers a, b, and If 5 + 7 = 8 + 4,
quantity and the second quantity c, if a = b, and b = c, then
Transitive and 8 + 4 = 12,
equals a third quantity, then the f rst a = c. then 5 + 7 = 12.
quantity equals the third quantity.
A quantity may be substituted for If a = b, then a may be
Substitution its equal in any expression. replaced by b in any If n = 15, then 3n = 3(15).
expression.
3