Page 105 - Math Course 2 (Book 2)

Transformations: Using Vectors

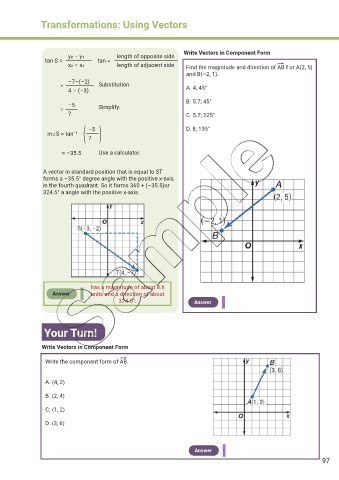
Write Vectors in Component Form
y2 – y1 length of opposite side
tan S = tan =
x2 – x1 length of adjacent side Find the magnitude and direction of AB f or A(2, 5)
and B(–2, 1).
–7–(–2)
= Substitution A. 4; 45°
4 – (–3)
B. 5.7; 45°
–5 Simplify.
=
7 C. 5.7; 225°
7 ( ) D. 8; 135°
–5
m∠S = tan ¹
–

≈ –35.5 Use a calculator.

A vector in standard position that is equal to ST
forms a –35.5° degree angle with the positive x-axis
in the fourth quadrant. So it forms 360 + (–35.5)or
324.5° a angle with the positive x-axis.

S(–3, –2)

T(4, –7)

has a magnitude of about 8.6
Answer units and a direction of about
324.5°. Answer

Your Turn!

Write Vectors in Component Form

Write the component form of AB.

A. 〈4, 2〉
B. 〈2, 4〉

C. 〈1, 2〉
D. 〈3, 6〉

Answer
97