Page 23 - Math Course 3 (Book 1)

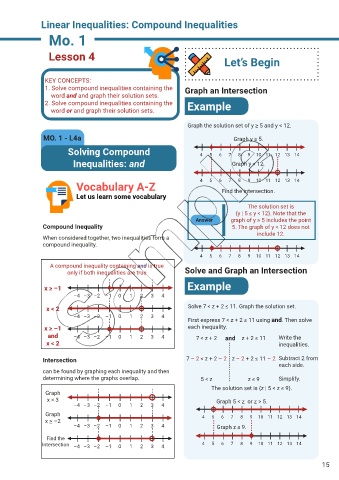
Linear Inequalities: Compound Inequalities
Mo. 1

Lesson 4 Let’s Begin

KEY CONCEPTS:
1. Solve compound inequalities containing the Graph an Intersection
word and and graph their solution sets.
2. Solve compound inequalities containing the Example
word or and graph their solution sets.

Graph the solution set of y ≥ 5 and y < 12.
MO. 1 - L4a Graph y ≥ 5.

Solving Compound 4 5 6 7 8 9 10 11 12 13 14
Inequalities: and Graph y < 12.

Vocabulary A-Z 4 5 6 7 8 9 10 11 12 13 14

Let us learn some vocabulary Find the intersection.
The solution set is
{y | 5 ≤ y < 12}. Note that the
Answer graph of y ≥ 5 includes the point
Compound Inequality 5. The graph of y < 12 does not
include 12.
When considered together, two inequalities form a
compound inequality.
4 5 6 7 8 9 10 11 12 13 14
A compound inequality containing and is true
only if both inequalities are true Solve and Graph an Intersection

x > –1 Example
–4 –3 –2 –1 0 1 2 3 4

x < 2 Solve 7 < z + 2 ≤ 11. Graph the solution set.
–4 –3 –2 –1 0 1 2 3 4
First express 7 < z + 2 ≤ 11 using and. Then solve
x > –1 each inequality.
and –4 –3 –2 –1 0 1 2 3 4 7 < z + 2 and z + 2 ≤ 11 Write the
x < 2 inequalities.

Intersection 7 – 2 < z + 2 – 2 z – 2 + 2 ≤ 11 – 2 Subtract 2 from
each side.
can be found by graphing each inequality and then
determining where the graphs overlap. 5 < z z ≤ 9 Simplify.
The solution set is {z | 5 < z ≤ 9}.
Graph
x < 3 Graph 5 < z or z > 5.
–4 –3 –2 –1 0 1 2 3 4
Graph 4 5 6 7 8 9 10 11 12 13 14
x > –2
–4 –3 –2 –1 0 1 2 3 4 Graph z ≤ 9.

Find the
Intersection –4 –3 –2 –1 0 1 2 3 4 4 5 6 7 8 9 10 11 12 13 14

15