Page 28 - Math Course 3 (Book 1)

Absolute Value Inequalities

Graphing Absolute Value Functions
Method 2 Compound Sentence
Examples
Write |t –1| = 5 as t – 1 = 5 or t – 1 = –5.
Case 1 Case 2
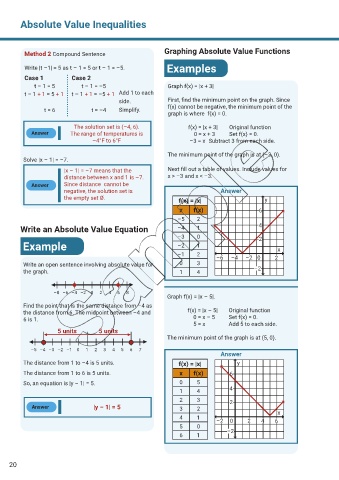
t – 1 = 5 t – 1 = –5 Graph f(x) = |x + 3|
t – 1 + 1 = 5 + 1 t – 1 + 1 = –5 + 1 Add 1 to each
side. First, find the minimum point on the graph. Since
t = 6 t = –4 Simplify. f(x) cannot be negative, the minimum point of the
graph is where f(x) = 0.

The solution set is {–4, 6}. f(x) = |x + 3| Original function
Answer The range of temperatures is 0 = x + 3 Set f(x) = 0.
–4°F to 6°F –3 = x Subtract 3 from each side.

The minimum point of the graph is at (–3, 0).
Solve |x – 1| = –7.
|x – 1| = –7 means that the Next fill out a table of values. Include values for
distance between x and 1 is –7. x > –3 and x < –3.
Answer Since distance cannot be
negative, the solution set is Answer
the empty set Ø. f(x) = |x| y

x f(x) 6
–5 2
Write an Absolute Value Equation –4 1 4
–3 0 2
Example –2 1 x

–1 2 –6 –4 –2 0 2
Write an open sentence involving absolute value for 0 3 –2
the graph. 1 4

–8 –6 –4 –2 0 2 4 6 8
Graph f(x) = |x – 5|.
Find the point that is the same distance from –4 as
the distance from 6. The midpoint between –4 and f(x) = |x – 5| Original function
6 is 1. 0 = x – 5 Set f(x) = 0.
5 = x Add 5 to each side.
5 units 5 units
The minimum point of the graph is at (5, 0).

–5 –4 –3 –2 –1 0 1 2 3 4 5 6 7
Answer
The distance from 1 to –4 is 5 units. f(x) = |x| y
The distance from 1 to 6 is 5 units. x f(x) 6
So, an equation is |y – 1| = 5. 0 5
1 4 4
2 3 2
Answer |y – 1| = 5 3 2

4 1 –2 0 2 4 6 x
5 0 –2
6 1

20