Page 135 - Math Course 2 (Book 2)

Triangle Properties of Inequalities

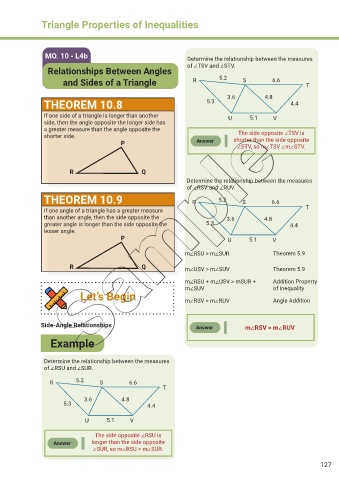
MO. 10 - L4b Determine the relationship between the measures

Relationships Between Angles of ∠TSV and ∠STV.

and Sides of a Triangle R 5.2 S 6.6 T

3.6 4.8
THEOREM 10.8 5.3 4.4

If one side of a triangle is longer than another U 5.1 V
side, then the angle opposite the longer side has
a greater measure than the angle opposite the
shorter side. The side opposite ∠TSV is
P Answer shorter than the side opposite
∠STV, so m∠TSV ∠m∠STV.

R Q
Determine the relationship between the measures
of ∠RSV and ∠RUV.
THEOREM 10.9 R 5.2 S 6.6

If one angle of a triangle has a greater measure T
than another angle, then the side opposite the 3.6 4.8
greater angle is longer than the side opposite the 5.3 4.4
lesser angle.
P U 5.1 V

m∠RSU > m∠SUR Theorem 5.9

R Q m∠USV > m∠SUV Theorem 5.9

m∠RSU + m∠USV > mSUR + Addition Property
m∠SUV of Inequality
Let’s Begin m∠RSV > m∠RUV Angle Addition

Side-Angle Relationships Answer m∠RSV > m∠RUV

Example

Determine the relationship between the measures
of ∠RSU and ∠SUR.

R 5.2 S 6.6
T

3.6 4.8
5.3 4.4

U 5.1 V

The side opposite ∠RSU is
Answer longer than the side opposite
∠SUR, so m∠RSU > m∠SUR.

127