Page 12 - Math Course 3 (Book 2)

Sum of the Angles of a Polygon

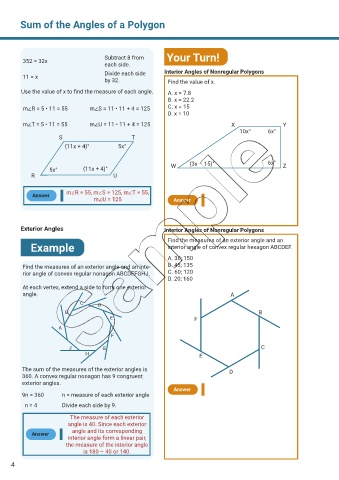
Subtract 8 from Your Turn!
352 = 32x
each side.
Divide each side Interior Angles of Nonregular Polygons
11 = x
by 32. Find the value of x.
Use the value of x to find the measure of each angle. A. x = 7.8
B. x = 22.2
m∠R = 5 • 11 = 55 m∠S = 11 • 11 + 4 = 125 C. x = 15
D. x = 10
m∠T = 5 • 11 = 55 m∠U = 11 • 11 + 4 = 125 X Y
10x° 6x°
S T
(11x + 4)° 5x°

5x° (11x + 4)° W (3x – 15)° 6x° Z
R U

m∠R = 55, m∠S = 125, m∠T = 55,
Answer
m∠U = 125 Answer

Exterior Angles Interior Angles of Nonregular Polygons

Find the measures of an exterior angle and an
Example interior angle of convex regular hexagon ABCDEF.

A. 30; 150
Find the measures of an exterior angle and an inte- B. 45; 135
rior angle of convex regular nonagon ABCDEFGHJ. C. 60; 120
D. 20; 160
At each vertex, extend a side to form one exterior
angle. A
C D
B B
E F
A
F

J G C
H E

The sum of the measures of the exterior angles is D
360. A convex regular nonagon has 9 congruent
exterior angles.
Answer
9n = 360 n = measure of each exterior angle
n = 4 Divide each side by 9.

The measure of each exterior
angle is 40. Since each exterior
angle and its corresponding
Answer
interior angle form a linear pair,
the measure of the interior angle
is 180 – 40 or 140.

4