Page 15 - Math Course 3 (Book 2)

Properties of Parallelograms

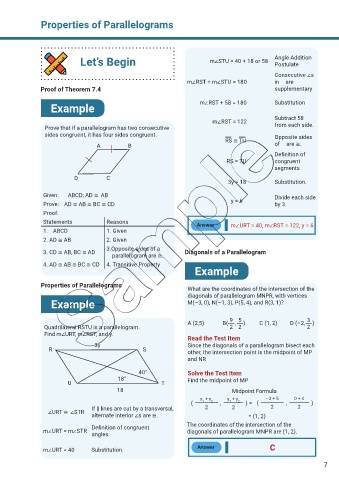
Let’s Begin m∠STU = 40 + 18 or 58 Angle Addition
Postulate

Consecutive ∠s
m∠RST + m∠STU = 180 in ▱ are
Proof of Theorem 7.4 supplementary

Example m∠RST + 58 = 180 Substitution

Subtract 58
m∠RST = 122
Prove that if a parallelogram has two consecutive from each side.
sides congruent, it has four sides congruent. Opposite sides
RS ≅ TU
A B of ▱ are ≅.
Definition of
RS = TU congruent
segments
D C
3y = 18 Substitution.

Given: ▱ABCD; AD ≅ AB Divide each side
Prove: AD ≅ AB ≅ BC ≅ CD y = 6 by 3.
Proof:
Statements Reasons
Answer m∠URT = 40, m∠RST = 122, y = 6
1. ▱ABCD 1. Given
2. AD ≅ AB 2. Given
3.Opposite sides of a
3. CD ≅ AB, BC ≅ AD Diagonals of a Parallelogram
parallelogram are ≅.
4. AD ≅ AB ≅ BC ≅ CD 4. Transitive Property
Example

Properties of Parallelograms
What are the coordinates of the intersection of the
diagonals of parallelogram MNPR, with vertices
Example M(–3, 0), N(–1, 3), P(5, 4), and R(3, 1)?

9 5
3
A (2,5) B( , ) C (1, 2) D (–2, )
Quadrilateral RSTU is a parallelogram. 2 2 2
Find m∠URT, m∠RST, and y.
Read the Test Item
3y Since the diagonals of a parallelogram bisect each
R S other, the intersection point is the midpoint of MP
and NR

40° Solve the Test Item
18° Find the midpoint of MP
U T
18 Midpoint Formula
x + x y + y –3 + 5 0 + 4
( 1 2 , 1 2 ) = ( , )
If || lines are cut by a transversal, 2 2 2 2
∠URT ≅ ∠STR
alternate interior ∠s are ≅. = (1, 2)
Definition of congruent The coordinates of the intersection of the
m∠URT = m∠STR diagonals of parallelogram MNPR are (1, 2).
angles.

m∠URT = 40 Substitution. Answer C

7