Page 150 - Math Course 1 (Book 2)

Measures of Variation

Mo. 11

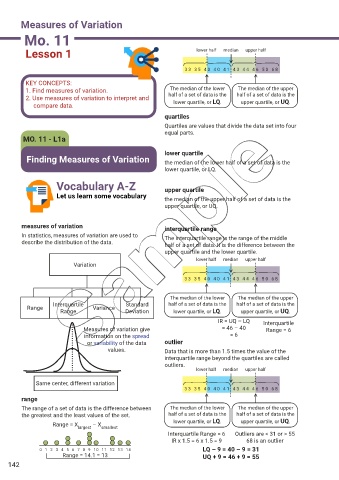
Lesson 1 lower half median upper half

33 35 40 40 4 1 4 3 4 4 4 6 5 0 68
KEY CONCEPTS:
1. Find measures of variation. The median of the lower The median of the upper
2. Use measures of variation to interpret and half of a set of data is the half of a set of data is the
compare data. lower quartile, or LQ. upper quartile, or UQ.

quartiles
Quartiles are values that divide the data set into four
equal parts.
MO. 11 - L1a

lower quartile
Finding Measures of Variation the median of the lower half of a set of data is the
lower quartile, or LQ.

Vocabulary A-Z upper quartile

Let us learn some vocabulary the median of the upper half of a set of data is the
upper quartile, or UQ.

measures of variation interquartile range
In statistics, measures of variation are used to The interquartile range is the range of the middle
describe the distribution of the data.
half of a set of data. It is the difference between the
upper quartile and the lower quartile.
lower half median upper half
Variation

33 35 40 40 4 1 4 3 4 4 4 6 5 0 68

The median of the lower The median of the upper
Interquartile Standard half of a set of data is the half of a set of data is the
Range Variance
Range Deviation lower quartile, or LQ. upper quartile, or UQ.
IR = UQ – LQ Interquartile
Measures of variation give = 46 – 40 Range = 6
information on the spread = 6
or variability of the data outlier
values. Data that is more than 1.5 times the value of the
interquartile range beyond the quartiles are called
outliers.
lower half median upper half

Same center, different variation
33 35 40 40 4 1 4 3 4 4 4 6 5 0 68
range
The range of a set of data is the difference between The median of the lower The median of the upper
the greatest and the least values of the set. half of a set of data is the half of a set of data is the
Range = X – X lower quartile, or LQ. upper quartile, or UQ.
largest smallest
Interquartile Range = 6 Outliers are < 31 or > 55
IR x 1.5 = 6 x 1.5 = 9 68 is an outlier
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 LQ – 9 = 40 – 9 = 31
Range = 14.1 = 13 UQ + 9 = 46 + 9 = 55
142